자연 변환

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
3. 성질
4. 예시
5. 역사
6. 응용
7. 초자연 변환
참조

1. 개요

자연 변환은 두 함자 사이의 사상으로, 범주론의 핵심 개념 중 하나이다. 구체적으로, 함자 F와 G가 주어졌을 때, 자연 변환은 모든 대상 X에 대해 사상 ηX: F(X) → G(X)을 포함하며, 이는 사상 f: X → Y에 대해 ηYF(f) = G(f)ηX를 만족시킨다. 자연 동형 사상은 모든 ηX가 동형 사상인 경우를 의미하며, 두 함자가 자연 동형이라는 것은 이들 사이에 자연 동형 사상이 존재함을 의미한다. 자연 변환은 수직 및 수평 합성을 가지며, 이러한 합성 연산은 항등원과 결합 법칙을 따른다. 자연 변환은 군론, 벡터 공간, 호몰로지 대수, 컴퓨터 과학 등 다양한 분야에 응용되며, 범주론의 발전에 중요한 역할을 했다.

더 읽어볼만한 페이지

함자 - 함자 (수학)
함자는 범주 C와 D 사이의 관계를 정의하는 수학적 개념으로, C의 대상과 사상을 각각 D의 대상과 사상에 대응시키며 항등 사상과 사상의 합성을 보존하고 다양한 종류와 성질을 가지며, 대수적 위상수학 등에서 발전했다.
함자 - 준층
준층은 작은 범주 C에 대한 집합 값 함자로, 데카르트 닫힌 범주이며 요네다 매장을 통해 범주 C를 포함하고, 모든 준층은 표현 가능 준층의 여극한으로 나타낼 수 있다.

자연 변환

2. 정의

$F,G\colon\mathcal C\to\mathcal D$ 가 (공변) 함자라고 할 때, $F$ 와 $G$ 사이의 '''자연 변환''' $\eta\colon F\Rightarrow G$ 는 다음 데이터로 구성된다.

모든 대상 $X\in\operatorname{ob}(\mathcal C)$ 에 대하여, 사상 $\eta_X\colon F(X)\to G(X)$

이 데이터는 다음 성질을 만족하여야 한다. 모든 사상

f\colon X\to Y

(

X,Y\in\operatorname{ob}(\mathcal C)

)에 대하여,

:

\eta_YF(f)=G(f)\eta_X

.

즉, 다음 그림이 가환하여야 한다.

마찬가지로, 반변함자 사이의 자연 변환도 정의할 수 있다.

'''자연 동형 사상'''(natural isomorphism^영어)은 모든

\eta_X

가 동형 사상을 이루는 자연 변환

\eta

이다. 두 함자 사이에 자연 동형 사상이 존재하는 경우, 두 함자가 '''자연 동형'''(naturally isomorphic^영어)이라고 한다.

3. 성질

세 함자 $F, G, H\colon \mathcal{C} \to \mathcal{D}$ 사이의 두 자연 변환 $\eta\colon F \Rightarrow G$, $\eta'\colon G \Rightarrow H$의 합성 $\eta' \circ \eta\colon F \Rightarrow H$는 다음과 같이 정의되며, 이는 자연 변환이다.^[2]

:$(\eta' \circ \eta)_X = \eta'_X \circ \eta_X$

두 함자 $F, G\colon \mathcal{C} \to \mathcal{D}$ 사이의 자연 변환 $\eta\colon F \Rightarrow G$ 및 함자 $T\colon \mathcal{D} \to \mathcal{E}$에 대하여, $T\eta\colon TF \Rightarrow TG$는 다음과 같이 정의되며, 이는 자연 변환이다.

:$(T\eta)_X = T(\eta_X)$

두 함자 $F, G\colon \mathcal{C} \to \mathcal{D}$ 사이의 자연 변환 $\eta\colon F \Rightarrow G$ 및 함자 $T\colon \mathcal{E} \to \mathcal{C}$에 대하여, $\eta T\colon FT \Rightarrow GT$는 다음과 같이 정의되며, 이는 자연 변환이다.

:$(\eta T)_X = \eta_{T(X)}$

자연 변환의 수직 합성은 결합 법칙을 따르며 항등원을 갖는다.^[2] 함자 $F$에 대한 항등 자연 변환 $\mathrm{id}_F$는 성분 $(\mathrm{id}_F)_X = \mathrm{id}_{F(X)}$를 갖는다. $\eta : F \Rightarrow G$에 대해, $\mathrm{id}_G \circ \eta = \eta = \eta \circ \mathrm{id}_F$이다.

자연 변환의 수평 합성은 항등원과 결합 법칙을 따른다.^[3] 항등원은 항등 펀터에 대한 항등 자연 변환이다. 범주 $\mathcal{C}$의 객체 $X$에 대해, $(\mathrm{id}_{\mathrm{id}_\mathcal{C}})_X = \mathrm{id}_{\mathrm{id}_\mathcal{C}(X)} = \mathrm{id}_X$이다. $\eta: F \Rightarrow G$에 대해, $F, G: \mathcal{C} \to \mathcal{D}$일 때, $\mathrm{id}_{\mathrm{id}_\mathcal{D}} * \eta = \eta = \eta * \mathrm{id}_{\mathrm{id}_\mathcal{C}}$이다.

휘스커링(Whiskering)은 펀터와 자연 변환 사이의 외부 이항 연산이다.^[4]^[5] $\eta: F \Rightarrow G$가 펀터 $F, G: \mathcal{C} \to \mathcal{D}$ 사이의 자연 변환이고, $H: \mathcal{D} \to \mathcal{E}$가 다른 펀터라면, 자연 변환 $H\eta: H \circ F \Rightarrow H \circ G$는 다음과 같이 구성된다.

:$(H\eta)_X = H(\eta_X)$.

반면에 $K: \mathcal{B} \to \mathcal{C}$가 펀터라면, 자연 변환 $\eta K: F \circ K \Rightarrow G \circ K$는 다음과 같이 정의된다.

:$(\eta K)_X = \eta_{K(X)}$.

수직 합성과 수평 합성은 상호 교환 법칙(Interchange law)을 만족한다.^[30] 만약 네 개의 자연 변환 $\alpha, \alpha', \beta, \beta'$가 있다면, 다음 항등식이 성립한다.

:$(\beta' \circ \alpha') * (\beta \circ \alpha) = (\beta' * \beta) \circ (\alpha' * \alpha)$.

4. 예시

군론에서, 군 $G$ 의 반대군 $G^{\operatorname{op}}$ 은 그 군 연산의 순서를 뒤집은 군이다. 이 "뒤집기"는 함자 $\mathrm{Grp}\to\mathrm{Grp}$ 를 이룬다. (여기서 $\mathrm{Grp}$ 는 군과 군 준동형의 범주다.) 이 함자는 항등함자 $\mathrm{Grp}\to\mathrm{Grp}$ 와 자연 동형이다. 이는 군의 반대군을 "자연스럽게" 정의할 수 있다는 것으로 해석할 수 있다.

(실수 또는 복소수) 유한 차원 벡터 공간 $V$ 는 그 쌍대 공간 $V^*$ 과 항상 동형이다. 그러나 이에 해당하는 함자 $\mathrm{FinVect}\to\mathrm{FinVect}$ 는 항등 함자와 자연 동형이지 않다. 이는 쌍대 공간을 정의하기 위해서는 기저를 골라야 하는데, 임의의 벡터 공간의 경우 자연스러운 기저를 정의할 수 없기 때문이다. (물론 기저는 항상 존재하나, 이를 자연스럽게 정의할 수 없다.) 물론, 유한 차원 내적공간의 범주의 경우, 쌍대 공간을 정의할 수 있는 데이터가 있으므로 쌍대 함자는 항등 함자와 자연 동형이다.

다음과 같은 진술이 있다.

: "모든 군은 자연스럽게 그 반대 군과 동형이다."

이것은 현대 수학에서 흔히 볼 수 있다. 이제 이 진술의 정확한 의미와 그 증명을 제시하겠다. 모든 군의 범주 $\textbf{Grp}$ 을 고려하고, 군 준동형을 사상으로 사용한다. $(G, *)$ 가 군이라면, 그 반대 군 $(G^\text{op}, {*}^\text{op})$ 을 다음과 같이 정의한다. $G^\text{op}$ 는 $G$ 와 동일한 집합이고, 연산 $*^\text{op}$ 는 $a *^\text{op} b = b * a$ 로 정의된다. 따라서 $G^{\text{op}}$ 의 모든 곱셈은 "뒤집힌다". 임의의 군 준동형 $f: G \to H$ 에 대해 $f^{\text{op}} = f$ 로 정의하면, 반대 군을 형성하는 것은 $\textbf{Grp}$ 에서 $\textbf{Grp}$ 로 가는 (공변) 함자가 된다. 다음을 유의하라.

$f^\text{op}$ 는 실제로 $G^\text{op}$ 에서 $H^\text{op}$ 로 가는 군 준동형이다.

: $f^\text{op}(a *^\text{op} b) = f(b * a) = f(b) * f(a) = f^\text{op}(a) *^\text{op} f^\text{op}(b).$

위 진술의 내용은 다음과 같다.

: "항등 함자 $\text{Id}_{\textbf{Grp}}: \textbf{Grp} \to \textbf{Grp}$ 는 반대 함자 ${\text{op}}: \textbf{Grp} \to \textbf{Grp}$ 와 자연 동형이다."

이것을 증명하기 위해, 위의 다이어그램이 교환되도록 모든 군 $G$ 에 대한 동형사상 $\eta_G: G \to G^{\operatorname{op}}$ 을 제공해야 한다.

$\eta_G(a) = a^{-1}$ 로 설정한다.

수식 $(a * b)^{-1} = b^{-1}*a^{-1}= a^{-1}*^{\text{op}} b^{-1}$ 와 $(a^{-1})^{-1} = a$ 는 $\eta_G$ 가 역 $\eta_{G^\text{op}}$ 를 갖는 군 준동형임을 보여준다. 자연성을 증명하기 위해, 군 준동형

$f : G \to H$ 로 시작하여 $\eta_H \circ f = f^{\text{op}} \circ \eta_G$ , 즉

$(f(a))^{-1} = f^\text{op}(a^{-1})$ for all $a$ in $G$ 임을 보여준다. 이것은 $f^{\text{op}} = f$ 이고 모든 군 준동형은 $(f(a))^{-1} = f(a^{-1})$ 속성을 갖기 때문에 참이다.

오른쪽 가군 $M$ 에서 $M^{\prime}$ 로 가는 $R$ -가군 준동형사상 $\varphi$ 가 있다고 하자. 모든 왼쪽 가군 $N$ 에 대해, 자연 사상 $\varphi \otimes N: M \otimes_{R} N \longrightarrow M^{\prime} \otimes_{R} N$ 이 존재하며, 이는 자연 변환 $\eta: M \otimes_{R} - \implies M' \otimes_{R} -$ 을 형성한다. 모든 오른쪽 가군 $N$ 에 대해, $\eta_{N}(f) = f\varphi$ 로 정의된 자연 사상 $\eta_{N}: \text{Hom}_{R}(M',N) \longrightarrow \text{Hom}_{R}(M,N)$ 이 존재하며, 이는 자연 변환 $\eta:\text{Hom}_{R}(M',-) \implies \text{Hom}_{R}(M,-)$ 을 형성한다.

주어진 군 $G$ 에 대해, 우리는 그 아벨화 $G^{\text{ab}} = G/$ $[G,G]$ 를 정의할 수 있다. $\pi_G: G \to G^{\text{ab}}$ 를 $[G,G]$ 의 잉여류로의 사영 사상으로 나타내자. 이 준동형 사상은 " $G$ 에서 자연스럽다," 즉, 자연 변환을 정의하며, 이를 지금 확인해 보자. $H$ 를 군이라고 하자. 임의의 준동형 사상 $f : G \to H$ 에 대해, $[G,G]$ 는 $\pi_H \circ f$ 의 커널에 포함되는데, 이는 아벨 군으로의 임의의 준동형 사상이 교환자 부분군을 죽이기 때문이다. 그러면 $\pi_H \circ f$ 는 유일한 준동형 사상 $f^{\text{ab}} : G^{\text{ab}} \to H^{\text{ab}}$ 에 대해 $f^{\text{ab}} \circ \pi_G = \pi_H \circ f$ 로 $G^{\text{ab}}$ 를 통해 인수분해된다. 이것은 ${\text{ab}} : \textbf{Grp} \to \textbf{Grp}$ 를 함자로 만들고, $\pi$ 를 항등 함자에서 $\text{ab}$ 로의 자연 변환으로 만들지만, 자연 동형 사상은 아니다.

대수적 위상수학에는 함수자와 자연 변환이 풍부하며, 후레비츠 준동형이 그 예시로 사용된다. 점있는 위상 공간 $(X,x)$ 과 양의 정수 $n$ 에 대해, 다음과 같은 군 준동형이 존재한다.

: $h_n \colon \pi_n(X,x) \to H_n(X)$

이는 $(X,x)$ 의 $n$ 차 호모토피 군에서 $X$ 의 $n$ 차 호몰로지 군으로 가는 준동형이다. $\pi_n$ 과 $H_n$ 은 모두 점있는 위상 공간 범주 '''Top^*'''에서 군 범주 '''Grp'''로 가는 함수이며, $h_n$ 은 $\pi_n$ 에서 $H_n$ 으로 가는 자연 변환이다.

가환환 $R$ 과 $S$ 가 환 준동형 $f : R \to S$ 를 가질 때, 각각의 가역 행렬 $n \times n$ 행렬 $\text{GL}_n(R)$ 과 $\text{GL}_n(S)$ 는 $f$ 를 각 행렬 성분에 적용하여 얻는 준동형을 상속하며, 이를 $\text{GL}_n(f)$ 로 표기한다. 마찬가지로, $f$ 는 $f^* : R^* \to S^*$ 로 제한되며, 여기서 $R^*$ 는 $R$ 의 단위군을 나타낸다. 사실, $\text{GL}_n$ 과 $*$ 는 가환환 범주 $\textbf{CRing}$ 에서 $\textbf{Grp}$ 로의 함자이다.

그룹 $\text{GL}_n(R)$ 에서의 행렬식은 $\text{det}_R$ 로 표기되며, 그룹 준동형이다.

: $\mbox{det}_R \colon \mbox{GL}_n(R) \to R^*$

이는 $R$ 에서 자연스럽다. 행렬식은 모든 환에 대해 동일한 공식으로 정의되므로, $f^* \circ \text{det}_R = \text{det}_S\circ \text{GL}_n(f)$ 가 성립한다. 이것은 행렬식을 $\text{GL}_n$ 에서 $*$ 로의 자연 변환으로 만든다.

예를 들어, $K$ 가 체인 경우, $K$ 위의 모든 벡터 공간 $V$ 에 대해 벡터 공간에서 이중 쌍대 공간으로 가는 "자연스러운" 단사 선형 사상 $V \to V^{**}$ 이 존재한다. 이러한 사상은 다음과 같은 의미에서 "자연스럽다": 이중 쌍대 연산은 함자이며, 사상은 항등 함자에서 이중 쌍대 함자로 가는 자연 변환의 성분이다.

모든 아벨 군 $G$ 에 대해, 정수에서 $G$ 의 기본 집합으로의 함수 집합 $\text{Hom}_\textbf{Set}(\mathbb{Z}, U(G))$ 은 점별 덧셈에 따라 아벨 군 $V_{\mathbb{Z}}(G)$ 을 형성한다. (여기서 $U$ 는 표준 망각 함자 $U:\textbf{Ab} \to \textbf{Set}$ 이다.)

$\textbf{Ab}$ 사상 $\varphi: G \to G'$ 가 주어지면, 이전의 원소들과 $\varphi$ 를 왼쪽으로 합성하여 얻는 맵 $V_\mathbb{Z}(\varphi): V_\mathbb{Z}(G) \to V_\mathbb{Z}(G')$ 는 그 자체로 아벨 군의 준동형 사상이다. 이런 방식으로 우리는 함자 $V_{\mathbb{Z}}: \textbf{Ab} \to \textbf{Ab}$ 을 얻는다. 각 함수 $f: \mathbb{Z} \to U(G)$ 를 $\Delta(f): n \mapsto f(n+ 1) - f(n)$ 로 보내는 유한 차분 연산자 $\Delta_G$ 는 $V_{\mathbb{Z}}(G)$ 에서 자신으로 가는 맵이며, 이러한 맵들의 모음 $\Delta$ 는 자연 변환 $\Delta: V_\mathbb{Z} \to V_\mathbb{Z}$ 를 제공한다.

아벨 군과 군 준동형 사상의 $\textbf{Ab}$ 범주를 고려해 보자. 모든 아벨 군 $X$ , $Y$ , $Z$ 에 대해 다음의 군 동형 사상이 존재한다.

: $\text{Hom}(X \otimes Y, Z) \to \text{Hom}(X, \text{Hom}(Y, Z))$ .

이러한 동형 사상은 두 개의 관련된 함자 $\textbf{Ab}^{\text{op}} \times \textbf{Ab}^{\text{op}} \times \textbf{Ab} \to \textbf{Ab}$ 사이의 자연 변환을 정의한다는 의미에서 "자연스럽다".

(여기서 "op"는 $\textbf{Ab}$ 의 반대 범주이며, $\textbf{Ab}$ 에 대한 자명한 반대 군 함자와 혼동해서는 안 된다!)

이것은 형식적으로 텐서-hom 수반이며, 한 쌍의 수반 함자의 전형적인 예이다. 자연 변환은 수반 함자와 함께 자주 발생하며, 실제로 수반 함자는 특정 자연 동형 사상에 의해 정의된다. 또한, 모든 한 쌍의 수반 함자는 ''단위''와 ''코단위''라고 불리는 두 개의 자연 변환(일반적으로 동형 사상이 아님)을 갖추고 있다.

모든 유한 차원 벡터 공간은 그 쌍대 공간과 동형이지만, 두 공간 사이에는 많은 다른 동형 사상이 있을 수 있다. 일반적으로 유한 차원 벡터 공간과 그 쌍대 공간 사이에는 자연스러운 동형 사상이 없다.^[1] 하지만, 관련 범주(추가적인 구조와 사상에 대한 제약 조건이 있는)는 아래에 설명된 대로 자연스러운 동형 사상을 갖는다.

유한 차원 벡터 공간의 쌍대 공간은 다시 같은 차원의 유한 차원 벡터 공간이며, 차원은 주어진 체 위의 유한 차원 벡터 공간의 유일한 불변량이므로 이들은 동형이다. 그러나 추가적인 제약 조건이 없는 경우(예: 사상이 선택된 기저를 보존해야 한다는 요구 사항), 공간에서 그 쌍대 공간으로의 사상은 유일하지 않으며, 따라서 그러한 동형 사상에는 선택이 필요하고, "자연스럽지 않다". 유한 차원 벡터 공간과 선형 사상의 범주에서, 각 공간에 대한 동형 사상을 선택하여(예를 들어, 모든 벡터 공간에 대한 기저를 선택하고 해당하는 동형 사상을 취함으로써) 벡터 공간에서 그들의 쌍대 공간으로의 준자연스러운 동형 사상을 정의할 수 있지만, 이것은 자연 변환을 정의하지 않을 것이다. 직관적으로 이것은 선택이 필요하기 때문이며, 엄밀히 말하면 그러한 동형 사상의 ''어떤'' 선택도, 예를 들어, 영 사상과 교환하지 않을 것이다.

유한 차원 벡터 공간(대상)과 항등 및 쌍대 함자에서 시작하여, 자연스러운 동형 사상을 정의할 수 있지만, 이를 위해서는 먼저 추가적인 구조를 추가한 다음, "모든 선형 사상"에서 "이 구조를 존중하는 선형 사상"으로 사상을 제한해야 한다. 명시적으로, 각 벡터 공간에 대해, 쌍대 공간으로의 동형 사상 $\eta_V\colon V \to V^*$ 의 데이터를 갖도록 요구한다. 다시 말해서, 비퇴화 쌍선형 형식 $b_V\colon V \times V \to K$ 을 가진 벡터 공간을 대상으로 취한다. 이것은 준자연스러운 동형 사상(각 객체에 대한 동형 사상)을 정의한다. 그런 다음 사상을 동형 사상과 교환하는 사상 $T\colon V \to U$ 만으로 제한한다: $T^*(\eta_{U}(T(v))) = \eta_{V}(v)$ 또는 다시 말해, 쌍선형 형식을 보존한다: $b_{U}(T(v),T(w))=b_V(v,w)$ . (이러한 사상은 동형 사상의 ''자연화자''를 정의한다.) 결과 범주는, 비퇴화 쌍선형 형식을 가진 유한 차원 벡터 공간을 대상으로 하고, 쌍선형 형식을 존중하는 선형 변환을 사상으로 하며, 각 공간이 쌍대 공간으로의 동형 사상을 가지고 범주의 사상이 교환하도록 요구되므로, 항등 함자에서 쌍대 함자로의 자연스러운 동형 사상을 구축한다. 이러한 관점에서 보면, 이 구성(각 객체에 대한 변환 추가, 이들과 교환하도록 사상 제한)은 완전히 일반적이며, 벡터 공간의 특정 속성에 의존하지 않는다.

이 범주(비퇴화 쌍선형 형식을 가진 유한 차원 벡터 공간, 쌍선형 형식을 존중하는 선형 변환을 사상으로 함)에서 벡터 공간 사이의 사상의 쌍대는 전치로 식별될 수 있다. 종종 기하학적 관심 때문에, 비퇴화 쌍선형 형식이 추가적인 속성, 예를 들어 대칭(직교 행렬), 대칭 및 양의 정부호(내적 공간), 대칭 세스퀴선형(에르미트 공간) , 반대칭 및 완전히 등방성(심플렉틱 벡터 공간) 등을 갖도록 요구함으로써 부분 범주로 특수화된다. – 이 모든 범주에서 벡터 공간은 비퇴화 쌍선형 형식에 의해 자연스럽게 쌍대 공간으로 식별된다.

집합 $X$ , $Y$ 에 대해, 집합의 데카르트 곱 $X \times Y$ 는 각 요소를 성분으로 갖는 순서쌍으로 구성된 집합 $\{(x,y)\mid x\in X, y\in Y\}$ 이다. 여기서, 세 개의 집합 $X$ , $Y$ , $Z$ 에 대해, $(X \times Y) \times Z$ 와 $X \times (Y \times Z)$ 두 집합을 생각한다. 두 집합은 분명히 순서쌍을 묶는 방식을 바꾼 것일 뿐이므로, 동형 $\alpha_{X,Y,Z}\colon(X\times Y)\times Z\cong X\times(Y\times Z)$ 을 얻는다. 이 동형은 더 나아가, $X$ , $Y$ , $Z$ 각각에 대해 자연스럽다. 즉, 사상 $\xi : X \to X^{\prime}$ , $\eta : Y \to Y^{\prime}$ , $\zeta : Z \to Z^{\prime}$ 에 대해 등식 $\alpha_{X',Y',Z'}\circ((\xi\times\eta)\times\zeta)=(\xi\times(\eta\times\zeta))\circ\alpha_{X,Y,Z}$ 이 성립한다. 이 사실은 위상 공간 범주 ^[13], 군 범주 $\textbf{Grp}$ , 작은 범주 범주 $\textbf{Cat}$ 등, 곱을 갖는 범주 일반^[14]에 성립한다.

체 $K$ 위의 벡터 공간 $V$ 에 대해, 쌍대 공간 $V^*$ 는 $V$ 에서 $K$ 로의 선형 사상 전체로 이루어진 벡터 공간이다. 이때, $V$ 에서 이중 쌍대 공간 $V^{$ } (즉, $V^*$ 에서 $K$ 로의 선형 사상으로 이루어진 공간)로의 단사 선형 사상 $\Psi_V: V \to V^{$ }가 다음 식에 의해 정의된다.

$\begin{alignat}{2}\Psi_V(x)\colon{}&V^*&\longrightarrow{}&K\\&\varphi&\longmapsto{}&\varphi(x)\end{alignat}$

더욱이 $V$ 가 유한 차원일 때, $\Psi_V$ 는 동형 사상이 된다. 분명히 $\Psi_V$ 는 $V$ 의 기저에 의존하지 않고 정의되므로, 역함수인 $\Psi_V^{-1}$ 역시 $V^{**}$ 의 기저에 의존하지 않는다. 이러한 의미에서 $\Psi_V$ 는 특별한 선형 사상이며, 또한 유한 차원의 경우에 대해 자연스럽다.^[15]

선형 사상 $f : V \to W$ 에 대해, $f^*: W^* \to V^*$ 는 $f^*\varphi(x)=\varphi(f(x))$ 에 의해 정의된다. 같은 연산을 한 번 더 수행하면, $f^{$ }: V^{} \to W^{}가 $f^{$ }X(\varphi)=X(f^*\varphi)로 정의된다. 정의에 의해, 준동형 사상의 합성에 대해 $(g\circ f)^{$ }=g^{}\circ f^{**}가 성립하므로, 이를 통해 이중 쌍대는 벡터 공간과 선형 사상으로 이루어진 범주 (벡터 공간의 범주 $\textbf{Vect}_K$ ) 위의 자기 함자임을 알 수 있다.

더욱이, 정의에 따라 계산하면 $f^{$ }(\Psi_V(x))(\varphi)=\varphi(f(x))를 얻으므로, $f^{$ }(\Psi_V(x))=\Psi_W(f(x))가 성립한다. 이상의 사실로부터, $\Psi_V$ 는 항등 함자와 이중 쌍대 함자 사이의 자연 변환 (유한 차원으로 제한한 경우에는 자연 동형)의 성분이 된다는 것을 알 수 있다.

위상 공간 $X$ 에 대해, $X$ 의 열린 집합 전체로 이루어진 집합 $O(X)$ 과 닫힌 집합 전체로 이루어진 집합 $C(X)$ 을 취하는 연산을 생각해보자. 연속 함수 $f: X \to Y$ 의 (서로 동치인) 정의로부터, $f$ 에 대해 열린 집합의 역상은 열린 집합으로, 닫힌 집합의 역상은 닫힌 집합으로 사상된다. 여기서부터 두 연산 $X \mapsto O(X)$ 와 $X \mapsto C(X)$ 는 반변관자 $O, C: \textbf{Top}^{\text{op}} \to \textbf{Set}$ 으로 간주할 수 있다.

위상 공간 $X$ 의 열린 집합 $U \in O(X)$ 에 대해, 그 여집합 $\overline{U}$ 은 닫혀 있으며, 또한 $\overline{U}$ 의 여집합은 $U$ 자신이다. 이로 인해 각 $O(X)$ 과 $C(X)$ 사이에 전단사를 정의할 수 있다. 이 전단사는 $X$ 에 대해 자연스러우며, 게다가 컴포넌트는 모두 동형이므로, $U$ 와 $C$ 사이에 자연 동형이 존재함을 알 수 있다.

아벨 군의 군 확대 $0 \to G \to E \overset{\beta}{\to} H \to 0$ 을 생각한다. 각 $h \in H$ 에 대해, $u(h) \in E$ 를 $1=\beta(u(h)) = h$ 를 만족하는 대표원으로 선택한다. 이 때, $E$ 의 각 요소는 $g + u(h)$ ( $g \in G$ ) 의 형태로 나타낼 수 있으며, 특히 $u(h) + u(k)$ 에 대해 $u(h)+u(k)=u(h+k)+f(h,k)\qquad(\exists f(h,k)\in G)$ 의 형태로 나타낼 수 있다. 이 때, $h, k \in H$ 로부터의 대응 $f$ 는, 아벨 군에서의 군 연산의 교환 법칙 및 결합 법칙으로부터, 다음 2 조건을 만족한다.

# $f(h,k)=f(k,h)$

# $f(h,k)+f(h+k,l)=f(h,k+l)+f(k,l)$

반대로, 사상 $f: H \times H \to G$ 가 위 2 조건을 만족할 때, 이를 $H$ 의 $G$ 에서의 factor set (인자단^[18])이라고 한다. 인자단에 대해, 다음 2가지 사실이 성립한다.

어떤 $H$ 의 $G$ 에서의 인자단 $f$ 는, 군 확대 $(E, \beta)$ 를 1개 결정한다^[19]
점별 가산 $(f_1+f_2)(h,k)=f_1(h,k)+f_2(h,k)$ 에 의해, 인자단의 집합 $\text{Fact}(G, H)$ 는 아벨 군을 이룬다^[20]

인자단에 의해 정해지는 군의 확대는 1대1 대응은 아니지만, 동치인 군의 확대를 정하는 인자단의 집합은

\text{Fact}(G, H)

상의 잉여류를 이루며, 결과적으로 군 확대들의 군

\text{Ext}(G, H)

를

\text{Fact}(G, H)

의 어떤 몫군으로 준다.

이하,

H

는 어떤 자유군

F

의 몫군

1=H = F/R

으로 한다. 전단과 마찬가지로,

h \in H

에 대해 대표원

u_0(h) \in F

를 선택하고, 그것에 의해 정해지는

H

의

R

에서의 인자단을

f_0

으로 나타낸다. 이 때, 준동형 사상

\theta: R \to G

에 대해

f_\theta(h,k)=\theta(f_0(h,k))

로 하면,

f_\theta

는

H

의

G

에서의 인자단이다. 이 대응은 더 나아가,

\text{Hom}(R, G)

에서

\text{Ext}(G, H)

로의 군 준동형 사상을 이룬다^[21]

지금, 자유군의 사이의 준동형 사상

T: F^{\prime} \to F

는

T(R^{\prime}) \subset R

를 만족한다고 한다. 이 때,

T

는

1=H^{\prime} = F^{\prime}/R^{\prime}

에서

1=H = F/R

로의 준동형 사상을 유도하며, 더 나아가 이것은 준동형 사상

T_e^*: \text{Ext}(G, H) \to \text{Hom}(G, H^{\prime})

를 이끌어낸다. 또한,

T

의 사전 합성

\theta\mapsto \theta\circ T

는 준동형 사상

T_h^*: \text{Hom}(R, G) \to \text{Hom}(R^{\prime}, G)

를 정한다.

이상의 설정 하에서,

\theta \mapsto f_\theta

가 정하는 인자단의 대응

\eta: \text{Hom}(R, G) \to \text{Ext}(G, H)

및

\eta^{\prime}: \text{Hom}(R^{\prime}, G) \to \text{Ext}(G, H^{\prime})

는

\eta'T_h^*=T_e^*\eta

를 만족한다^[22] 이 의미에서

\eta

는 자연스러운 대응이다.

보수

\lnot a

를 갖는 분배 격자

(B, \le, 0, 1, \land, \lor, \lnot)

를 부울 대수라고 한다. 두 점 집합

1=2 = \{0, 1\}

에 적절한 연산을 넣은 것은 최소 부울 대수의 구성이 된다. 부울 대수의 준동형사상

f : A \to B

는 사상

f : A \to B

로 각 연산의 결과를 보존하는 것을 말한다.

부울 대수

(B, \le, 0, 1, \land, \lor, \lnot)

의 초필터 (우르트라필터)는

B

의 부분 집합

U \subset B

로,

공집합이 아니고 (특히, 1을 포함)
만남 ∧에 대해 닫혀 있고 (이면 이다)
의 상위 집합은 의 부분을 이룬다 (이고 이면 이다)
는 극대이다 (위 3가지 조건을 만족하는 가 존재한다면, 이다)

를 만족하는 것이다^[23]。이때,

B

의 울트라필터는

B

에서 2로의 준동형사상과 일대일 대응한다^[24]。

부울 대수와 그 사이의 준동형사상으로 이루어진 범주를

\textbf{BA}

로 나타낸다. 이 때, 대응

B\mapsto\mathop{\mathrm{Hom}_{\mathbf{BA}}}(B,2)

는

\textbf{BA}

에서 집합의 범주로의 반변 관자

\mathop{\mathrm{Hom}_{\mathbf{BA}}}(\_,2):\mathbf{BA}^{\mathrm{op}}\to\mathbf{Set}

를 구성한다. 한편, 부울 대수의 준동형사상

h : A \to B

와

B

의 울트라필터

U

에 대해, 역상

h^{-1}U \subset A

는

A

의 울트라필터이므로, 이것으로 사상

\text{Ult}(h): \text{Ult}(B) \to \text{Ult}(A)

를 얻는다 (로

B

의 울트라필터의 집합을 나타낸다). 이것은

\textbf{BA}

에서

\textbf{Set}

로의 반변 관자이며, 또한 동형

\mathop{\mathrm{Ult}}(B)\cong\mathop{\mathrm{Hom}_{\mathbf{BA}}}(B,2)

는

B

에 대해 자연스럽다^[25]。

쌍대 벡터 공간을 취하는 연산은 보통 반변 함자

\textbf{Vect}_K^{\text{op}} \to \textbf{Vect}_K

로 간주된다 (이때

f : V \to W

에 대해

f^*: W^* \to V^*

는 앞서 언급한

f^*\varphi(x)=\varphi(f(x))

로

5. 역사

사무엘 에일렌베르크와 손더스 매클레인이 1945년에 자연 변환을 도입하였다.^[39]^[40] 이 논문은 범주론의 시초로 여겨진다. 에일렌베르크와 매클레인은 "범주를 정의한 이유는 함자를 정의하기 위해서이고, 함자를 정의한 이유는 자연 변환을 정의하기 위해서이다."라고 언급했다.

샌더스 맥레인은 "나는 펀터를 연구하기 위해 범주를 발명한 것이 아니라, 자연 변환을 연구하기 위해 발명했다."라고 말한 것으로 알려져 있다.^[7] 군 연구가 준동형 사상 연구 없이는 불완전하듯이, 범주 연구 또한 펀터 연구 없이는 불완전하며, 펀터 연구 자체가 자연 변환 연구 없이는 불완전하기 때문이다.

맥레인의 발언의 배경은 호몰로지의 공리적 이론이었다. 호몰로지를 구성하는 다양한 방법들이 일치한다는 것을 보일 수 있었다. 예를 들어 단순 복합체의 경우, 직접 정의된 군은 특이 이론의 군과 동형이다. 자연 변환의 언어 없이는 호몰로지 군이 대상 간의 사상과 어떻게 호환되는지, 그리고 두 개의 동치 호몰로지 이론이 동일한 호몰로지 군뿐만 아니라 해당 군 간의 동일한 사상도 가지는지를 쉽게 표현할 수 없다.

자연 변환은 1940년대 초 수학자들이 비형식적으로 사용하던 "자연스러운" 동형 또는 "자연스러운" 동상 사상의 개념을 정식화하기 위해 1942년에 아일렌버그와 맥레인에 의해 도입되었다.^[27]^[28] 1945년에는 이 두 사람에 의해 "General Theory of Natural Equivalences" (자연 동치의 일반 이론)가 발표되었고, 이를 통해 자연 변환의 이론이 정식화되었다. 1940년대 후반에는 호몰로지론이나 추상대수 분야에서 이 개념이 적용되기 시작했고, 이후 그로텐디크 등에 의해 대수기하에, 로베어 등에 의해 논리학에, 그 후에도 컴퓨터 과학, 언어학, 인지 과학, 철학 등의 다양한 분야에서 응용 사례가 나타나게 되었다.^[29]

맥레인은 『범주론의 기초』에서 "범주는 함자를 정의 가능하게 하기 위해 정의되었으며, 함자는 자연 변환을 정의 가능하게 하기 위해 정의되어 왔다"라고 적었다.

6. 응용

자연 변환은 범주론의 핵심 개념으로, 수학의 여러 분야에 널리 응용된다.

대수적 위상수학, 호몰로지 대수, 표현론: 이들 분야에서 자연 변환은 중요한 역할을 한다.
컴퓨터 과학, 논리학, 언어학, 인지 과학, 철학: 자연 변환은 이들 분야에도 응용된다.

함자 범주는 함자를 대상으로 하고, 자연 변환을 사상으로 갖는 범주이다. 이 범주에서 극한과 쌍대극한 등의 개념을 정의할 수 있다. 특히, 극한과 쌍대극한은 함자 범주 내에서 보편 사상으로 나타낼 수 있다.

요네다 보조정리는 표현 가능 함자와 관련된 중요한 정리이다. 이 정리는 표현 가능 함자에서 임의의 함자로 가는 자연 변환을 쉽게 설명할 수 있게 해준다.^[32] 요네다 보조정리는 범주론에서 매우 중요하며, 다양한 결과를 도출하는 기본적인 정리로 평가받는다.

7. 초자연 변환

범주 '''A''', '''B''', '''C''', '''D'''와 함자, 에 대하여, 에서 로의 '''초자연 변환'''(Extranatural transformation) 는 , , 로 매개변수화된 사상의 족 로, 임의의 사상 , , 에 대하여 다음의 도식이 가환이 되는 것을 말한다.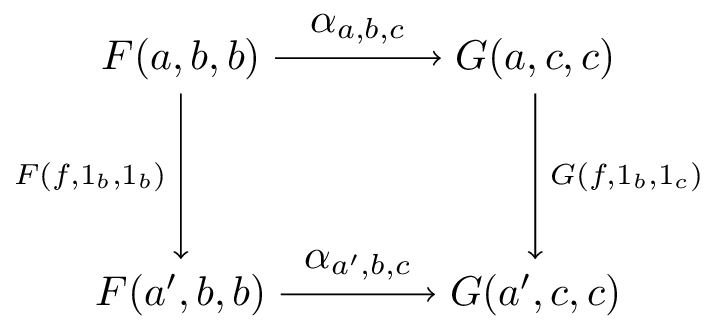

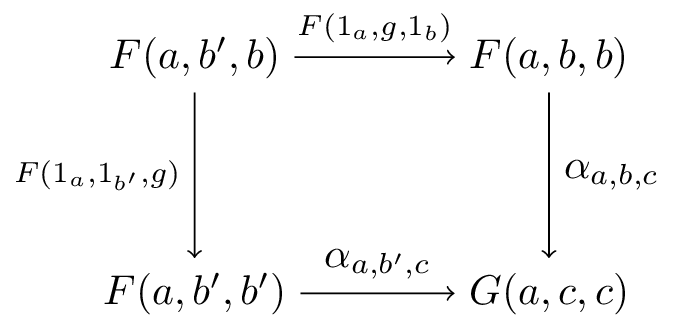
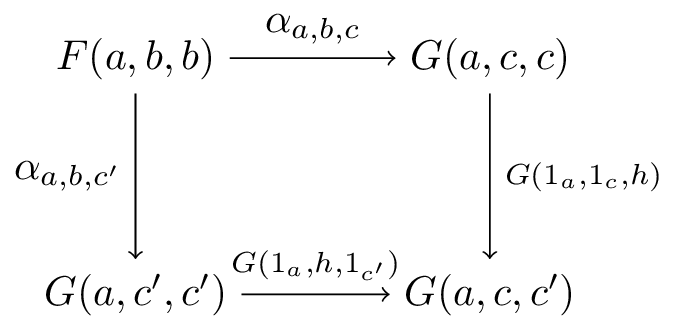
각 가환 도식은 에 대한 자연성, 과 의 각각 및 에 대한 특별 자연성을 나타낸다.^[37]

초자연 변환 중 특히 어느 한쪽이 상수 함자인 경우, 특수한(여)극점으로서 엔드 및 코엔드가 정해진다. 엔드나 코엔드는 hom 함자와 관련성이 있으며, 예를 들어 풍요로운 범주론에서는 풍요로운 범주의 「함자 범주」를 정의하기 위해 엔드를 사용한다.^[38]

참조

_[1] 서적 §VI.4 1999
_[2] 웹사이트 Identity natural transformation in nLab https://ncatlab.org/[...]
_[3] 웹사이트 Natural Transformations https://bartoszmilew[...] 2015-04-07
_[4] 웹사이트 Definition:Whiskering - ProofWiki https://proofwiki.or[...]
_[5] 웹사이트 Whiskering in nLab https://ncatlab.org/[...]
_[6] 논문 p. 38 https://arxiv.org/pd[...]
_[7] 서적 §I.4 1998
_[8] 서적 map between functors 2014
_[9] 문서 対象の族 {{math|{''S''_''x''}_{''x'' ∈ ''C''}}}、{{math|{''T''_''x''}_{''x'' ∈ ''C''}}} が関手を構成することも条件に含む
_[10] 서적 1998
_[11] 서적 1990
_[12] 서적 1990
_[13] 서적 1945
_[14] 서적 2010
_[15] 서적 ... “natural” in that it is given ''simultaneously'' for ''all'' finite-dimensional vector spaces {{Mvar|L}}. 1945
_[16] 서적 2016
_[17] 서적 2016
_[18] 서적 名称は 2013
_[19] 서적 1942
_[20] 서적 1942
_[21] 서적 1942
_[22] 서적 1942
_[23] 서적 定義は 2010
_[24] 서적 2010
_[25] 서적 2010
_[26] 서적 1945
_[27] 서적 1942
_[28] 서적 By the early 1940s, researchers in algebraic topology had started to use the phrase ‘natural transformation’, but only in an informal way. Two mathematicians, Samuel Eilenberg and Saunders Mac Lane, saw that a precise definition was needed. 2014
_[29] 서적 2010
_[30] 서적 1998
_[31] 서적 例えば 2021
_[32] 서적 2016
_[33] 서적 2012
_[34] 서적 2003
_[35] 서적 1963
_[36] 논문
_[37] 논문
_[38] 서적
_[39] 저널 General theory of natural equivalences 1945-09
_[40] 서적 Stanford Encyclopedia of Philosophy Metaphysics Research Lab, Stanford University 2010-02-25
_[41] 서적 Categories for the working mathematician Springer 1998

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com